价值工程在空调工程方案优选中的改进与应用
摘要:在价值工程原理的基础上,将层次分析法的思想引入到价值工程中来,发展创新了价值工程在工程方案优化选择中的应用,为工程中多方案选择问题提出了一套客观简捷的方法,并通过空调工程多方案选择的实际案例,证实了价值工程和层次分析法的有机结合能较为客观的评价方案的优劣。
关键词:价值工程;层次分析法;方案优选
方案的优化选择问题是目前各类工程实施过程中普遍面临的问题,但是由于方案指标的多样性及不确定性,还不能利用数学模型进行理论上的优化,应用最多的是集中多个专家或决策者对方案进行论证、评比和选择,但因个人的经验、知识及偏好的差异,完全有可能导致方案的不一致或不合理。价值工程,又称价值分析,是通过各相关领域的协作,对所研究对象的功能与成本进行系统分析,不断创新,旨在提高所研究对象价值的思想方法和管理技术[1]。本文以价值工程为基础对污水处理厂建设的多方案选择问题进行优化,并成功的将层次分析法的思想引入到价值工程中来,创新价值工程的同时为工程方案的优化提出了一套客观简捷的方案。
1.价值工程的原理
价值工程是运用集体智慧和有组织的活动,着重对产品进行功能和成本分析,使之以最低的总成本,可靠的实现产品必要的功能,从而提高产品价值的一套科学的技术经济分析方法。它的基本思想是在可靠地实现使用者所需功能的前提下, 努力寻求寿命周期成本最低的创新方案, 以达到合理、有效地利用资源、提高对象价值的目的, 这正是价值工程的实质[1] [2]。
在多方案比较选优中运用价值工程分析, 可用价值系数的方法来综合评价各方案的性能并进行决策, 其计算公式如下:
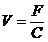
式中: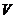 为价值系数;
为价值系数;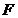 为功能系数;
为功能系数;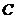 为成本系数。
为成本系数。
价值工程是分析产品功能和成本的关系,力求以最低的成本实现产品必要功能的一种有组织的的活动和管理方法,产品或作业的价值越大,表明了资源利用的越好[3]。在方案优化选择问题中,需用评价指标对项目进行评价,根据评价指标期望值的不同,将评价指标分为成本型指标和功能型指标。成本型指标是指像工程投资、占地面积等数值愈小愈好的指标;而功能型指标是指像对城市发展的适应性、分期实施的可能性等愈大愈好的指标,用成本型指标和功能型指标可分别求出每个方案的成本系数和功能系数,进而求出方案的价值系数,从而判断方案的优劣。
2.系数方程的建立及求解
2.1指标特征量矩阵的确定
工程项目中的多方案优化选择问题可视为有限个方案多目标决策问题[4]。设共有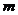 个待选方案,每个方案有
个待选方案,每个方案有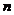 个评价指标,以待选方案为行标
个评价指标,以待选方案为行标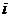 ,以评价指标为列标
,以评价指标为列标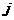 ,写出各个方案各评价指标的评价值矩阵
,写出各个方案各评价指标的评价值矩阵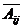 =
= (
(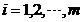 ,
,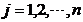 )。
)。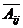 即为指标特征量矩阵:
即为指标特征量矩阵:
 =
=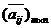 =
=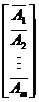 =
=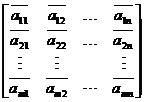
式中: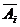 (
(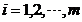 )表示第
)表示第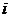 个方案的指标特征量行向量。在构造特征量矩阵时,对于确定性指标,如工程造价、占地面积等以实际数值表示,对于不确定指标,如维护管理的可操作性、部分负荷是的能效比等可采用模糊数学中的5级划分法进行评定,即将指标的性能分成优、良、中、差、劣5个等级进行描述,在构造特征量矩阵时分别用其相对应的隶属度0.9、0.7、0.5、0.3、0.1进行量化,旨在建立一个全数字形式的特征量矩阵[4] [5] [6]。
个方案的指标特征量行向量。在构造特征量矩阵时,对于确定性指标,如工程造价、占地面积等以实际数值表示,对于不确定指标,如维护管理的可操作性、部分负荷是的能效比等可采用模糊数学中的5级划分法进行评定,即将指标的性能分成优、良、中、差、劣5个等级进行描述,在构造特征量矩阵时分别用其相对应的隶属度0.9、0.7、0.5、0.3、0.1进行量化,旨在建立一个全数字形式的特征量矩阵[4] [5] [6]。
2.2特征量矩阵的无量纲化
由于各指标往往具有不同的量纲,且数值差距较大,若直接对特征量矩阵进行计算的话,计算困难且可能对决策结果产生影响,因此,需对特征量矩阵进行无量纲化处理。具体的方法为特征量矩阵中的各行向量同除去该矩阵中的任意一个行向量,即得到的无量纲化矩阵为某一行向量值全为1的矩阵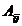 。
。
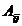 =
= =
=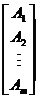 =
=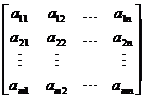
式中: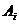 (
( )表示第
)表示第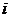 个方案的指标特征量无量纲行向量。
个方案的指标特征量无量纲行向量。
2.3指标权重矩阵的构造
构造指标权重矩阵是层次分析法求指标权重的关键步骤,可采用对全体评价指标进行两两比较的遍历法。由多个专家对各项指标的重要性进行两两比较并将比较的结果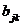 (
(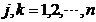 )写成
)写成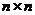 阶矩阵
阶矩阵 的形式:
的形式:
 =
=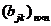 =
= =
=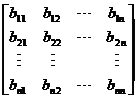
式中 表示第
表示第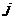 项指标与第
项指标与第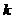 项指标相比的重要程度,为将结果以数字的形势表示出来,可采用1—9比例标度法,其比例标度及含义如表1所示:
项指标相比的重要程度,为将结果以数字的形势表示出来,可采用1—9比例标度法,其比例标度及含义如表1所示:
表1 指标权重矩阵的比例标度及含义
|
标度 |
含义 |
|
1 |
表示指标j与k指标相比,j与k同等重要 |
|
3 |
表示指标j与k指标相比,j比k稍显重要 |
|
5 |
表示指标j与指标k相比,j比k明显重要 |
|
7 |
表示指标j与指标k相比,j比k强烈重要 |
|
9 |
表示指标j与指标k相比,j比k极端重要 |
|
2,4,6,8 |
分别表示为相邻1—3,3—5,5—7,7—9的中值 |
|
1/(1~9) |
表示指标k与j比较的值 |
显然,在指标权重矩阵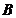 中,主对角线上的值都为1,且一个值与该值的倒数关于主对角线对称,即
中,主对角线上的值都为1,且一个值与该值的倒数关于主对角线对称,即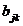 =
=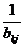 (
(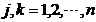 )。
)。
2.4指标权重的求解
求各指标的的权重即求由2.3构造的指标权重矩阵最大特征值对应的特征向量,可用归一化法求解:
1)将指标权重矩阵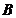 的各列作归一化处理:
的各列作归一化处理: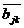 =
=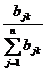 (
(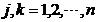 )
)
2)求指标权重矩阵各列元素之和: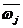 =
=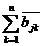 (
(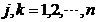 )
)
3)对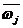 作归一化处理得到
作归一化处理得到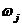 :
: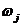 =
=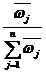 (
( )
)
则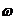 =
=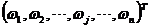 即为所求的
即为所求的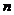 个指标所对应的权值向量,显然有
个指标所对应的权值向量,显然有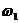 +
+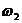 +…+
+…+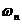 =1。指标权重向量可分解为成本指标权重向量
=1。指标权重向量可分解为成本指标权重向量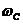 和功能指标权重向量
和功能指标权重向量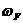 之和,即
之和,即 (成本指标权重向量中所有的功能指标权重取零值,功能指标权重向量中所有的成本指标权重取零值)。
(成本指标权重向量中所有的功能指标权重取零值,功能指标权重向量中所有的成本指标权重取零值)。
2.5指标权重矩阵的一致性检验
在专家构造指标权重矩阵时,不可避免的会产生认识上的不一致,因此,需对指标权重矩阵进行一致性检验,经过检验的结果,方可认为是可行的。具体检验方法如下:
1)根据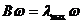 求出指标权重矩阵的最大特征值
求出指标权重矩阵的最大特征值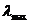 :
: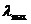 =
=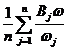 (
(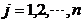 )
)
2)计算一致性指标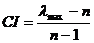 ,式中
,式中 为评价指标的个数
为评价指标的个数
3)查表2找出相应阶数的的平均随机一致性指标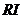
4)按照式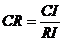 计算一致性比率
计算一致性比率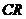
当一致性比率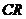 <0.1时,认为指标权重矩阵
<0.1时,认为指标权重矩阵 基本符合随机一致性指标;当
基本符合随机一致性指标;当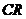 ≥0.1时,则认为指标权重矩阵不符合随机一致性指标,须对该矩阵进行调整使其满足
≥0.1时,则认为指标权重矩阵不符合随机一致性指标,须对该矩阵进行调整使其满足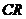 <0.1。
<0.1。
表2 1阶~15阶的平均随机一致性指标表
|
阶数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
RI |
0 |
0 |
0.52 |
0.89 |
1.12 |
1.26 |
1.36 |
1.41 |
|
阶数 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
RI |
1.46 |
1.49 |
1.52 |
1.54 |
1.56 |
1.58 |
1.59 |
|
2.6功能系数和成本系数的确定
成本系数和功能系数可由无量化的特征量矩阵和相应的指标权重向量求出,具体方法如下:
成本系数等于各方案指标特征量无量纲行向量乘以成本指标权重向量的值,即
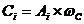 (1)
(1)
功能系数等于各方案指标特征量无量纲行向量乘以功能指标权重向量的值,即
 (2)
(2)
式中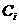 、
、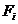 分别表示第
分别表示第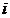 个方案的成本系数和功能系数。
个方案的成本系数和功能系数。
2.7价值系数的确定和最佳方案的选择
各方案价值系数等于该方案功能系数除该方案成本系数的值,即
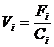 (3)
(3)
式中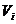 分别表示第
分别表示第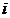 个方案的价值系数。价值系数大的方案,具有功能强、价格低的特点,即为所有待选方案中最好的方案。
个方案的价值系数。价值系数大的方案,具有功能强、价格低的特点,即为所有待选方案中最好的方案。
3.应用举例
某单位食堂建筑面积2300 m2,空调面积2000 m2,单位面积空调冷负荷值310W/ m2,总冷负荷620kW,按甲方要求设中央空调系统,现有如下三种方案:螺杆机组+冷却塔+循环水泵+风机盘管(方案一)、风冷热泵+循环水泵+风机盘管(方案二)、多联机中央空调(方案三)[6]。
先用以上方法确定最佳方案,其评价指标为:空调方案对使用功能的适应性(I1)、工程造价(万元,I2)、年运行费用(元/年,I3)、维护管理可操作性(I4)、设备使用寿命(I5);具体评价指标如表三所示:
表3 空调方案评价指标表
|
方案 |
I1 |
I2 |
I3 |
I4 |
I5 |
|
方案一 |
中 |
124.1 |
85987 |
良 |
良 |
|
方案二 |
优 |
127.4 |
104011 |
良 |
良 |
|
方案三 |
优 |
122.0 |
42408 |
优 |
优 |
1.根据上表确定指标特征量矩阵如下:
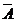 =
=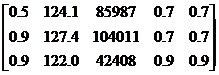
2.将指标特征量矩阵进行无量纲化处理得:
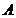 =
=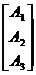 =
=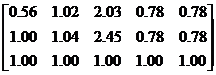
3.对全体指标的重要性进行两两比较,结果如表4所示:
表4 指标重要性比较表
|
指标 |
I1 |
I2 |
I3 |
I4 |
I5 |
|
I1 |
1 |
1/3 |
1/2 |
1/4 |
1/5 |
|
I2 |
3 |
1 |
2 |
1/2 |
1/3 |
|
I3 |
2 |
1/2 |
1 |
1/3 |
1/3 |
|
I4 |
4 |
2 |
3 |
1 |
1/2 |
|
I5 |
5 |
3 |
3 |
2 |
1 |
由上表写出指标权重矩阵 :
:
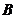 =
=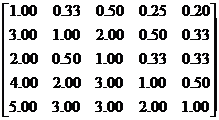
4.归一化处理后得:
 =
=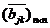 =
=
对其各行元素求和可得:
 =2.094,
=2.094, =0.814,
=0.814,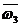 =1.250,
=1.250,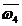 =0.500,
=0.500,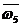 =0.317
=0.317
对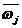 做归一化处理后得到所有指标的权值向量
做归一化处理后得到所有指标的权值向量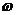 :
:
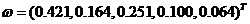
在所有的六项指标中第2、3、5项为成本型指标,其余为功能型指标,可得
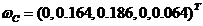
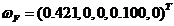
5.矩阵 的最大特征值向量
的最大特征值向量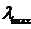 =5.381,当
=5.381,当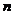 =5,计算其一致性指标
=5,计算其一致性指标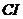 =0.0967,由表2可查出
=0.0967,由表2可查出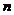 =5的平均随机一致性指标
=5的平均随机一致性指标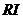 =1.12,代入公式求出一致性比率
=1.12,代入公式求出一致性比率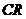 =0.085<0.1,所以判断矩阵
=0.085<0.1,所以判断矩阵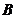 符合随机一致性指标。
符合随机一致性指标。
6.将以上求出的数值代入式(1)(2)(3)可求出各个方案的价值系数分别为: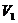 =0.432,
=0.432,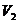 =0.597,
=0.597,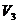 =1.088。显然
=1.088。显然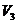 >
> >
> ,即三种工艺方案的优先顺序为:方案三→方案二→方案一。
,即三种工艺方案的优先顺序为:方案三→方案二→方案一。
4.结论与建议
价值工程法把技术先进性与经济合理性统一起来进行技术评价,这样就使得技术评价更加科学合理。但由于采用强制确定法,而使评价仍具有一定的主观性,将层次分析法的思想引入到价值工的运用中来,通过指标权重矩阵的建立和一致性检验可在一定程度上减少主观因素的影响,从而能够较为客观的评判选择出社会效益与经济效益最优的方案。
参考文献
[1]陶燕瑜.工程技术经济[M].重庆:重庆大学出版社,2002.
[2] 张健,郭剑峰,李慧民等.基于价值工程的改扩建项目投资决策分析[J].西安建筑科技大学学报(自然科学版),2007,39(5):635-640.
[3] 姚胜,贾仁甫,张炯.价值工程在地块开发方案优选中的应用[J].价值工程,2007,26(2):79-80.
[4]王浙明,史惠祥,苏雨生等.灰色关联模型用于工程方案优化[J].中国给水排水,2002,18(1):81-84.
[5] 焦树锋.AHP法中平均随机一致性指标的算法及MATLAB实现[J].太原师范学院学报(自然科学版),2006,5(4):45-47.
[6] 陆妍杰.多联机空调与集中式中央空调方案设计比较[J].暖通制冷设备,2010,4:16-18.

